INVERS FUNGSI
Suatu fungsi dengan sifat tertentu memiliki invers, fungsi tersebut adalah fungsi yang memiliki sifat bijektif atau korespondensi satu-satu. Begitu juga dengan komposisi fungsi. Komposisi dari dua buah fungsi yang memiliki invers juga akan memiliki invers. Perhatikan pengertian invers yang dijelaskan melalui gambar di bawah untuk membantu pemahaman.
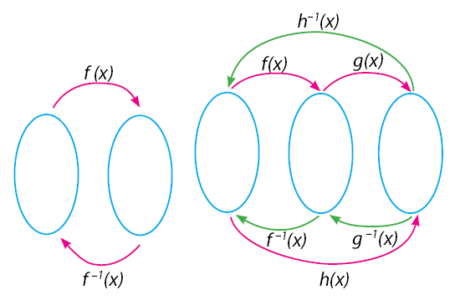
Misalkan suatu fungsi  memiliki invers
memiliki invers  dan
dan  memiliki invers
memiliki invers  . Komposisi
. Komposisi  dan
dan  juga akan memiliki invers. Komposisi invers ini memiliki sifat fungsi invers yang akan dijelaskan kemudian.
juga akan memiliki invers. Komposisi invers ini memiliki sifat fungsi invers yang akan dijelaskan kemudian.
Pada gambar sebelah kiri ditunjukkan sebuah fungsi  yang memiliki fungsi invers
yang memiliki fungsi invers  . Gambar di sebelah kanan adalah komposisi dua buah fungsi dan inversnya.
. Gambar di sebelah kanan adalah komposisi dua buah fungsi dan inversnya.
Sebelum membahas mengenai sifat invers pasa komposisi fungsi. Kita akan mempelajari terlabih dahulu proses mencari invers dari suatu fungsi. Penjelasan akan disajikan dalam bentuk soal dan pembahasan, jadi simak soal dan pembahasan tentang invers fungsi di bawah dengan baik.
Tentukan invers dari fungsi f(x) di bawah!
Pembahasan:
Misalkan f(x) = y, maka
Berdasarkan persamaan akhir di atas dapat disimpulkan bahwa fungsi invers dari f(x) adalah
Bagaimana, mudah bukan?
Cara menentukan invers suatu fungsi, seperti cara di atas, memang cukup panjang. Sebenarnya, ada rumus praktis untuk menentukan suatu fungsi invers. Meskipun demikian, sebaiknya sudah menguasai konsep pencarian invers suatu fungsi di atas terlebih dahulu. Hal ini akan bermanfaat untuk sobat nantinya, juga akan bermanfaat ketika lupa rumus cepatnya.
Cara cepat mencari sebuah fungsi invers untuk bentuk tertentu dapat diperoleh dengan cara berikut.

Kita akan menggunakan cara cepat mencari invers fungsi untuk menyelesaikan persoalan yang sama pada soal dan pembahasan invers fungsi di atas.
Bagaimana? Hasilnya sama bukan dengan cara sebelumnya? Selanjutnya kita akan mempelajari sifat invers suatu fungsi.
Sifat Invers pada Komposisi Fungsi
Pembahasan sifat invers pada komposisi fungsi mempelajari hubungan kesamaan suatu fungsi invers dengan kesamaan lainnya. Sifat invers pada komposisi fungsi dapat membuat lebih tepat dalam menentukan langkah yang tepat untuk menyelesaikan variasi soal yang diberikan terkait komposisi fungsi.
Sifat Fungsi Invers pada komposisi fungsi dapat dilihat pada gambar di bawah.

Contoh Soal dan Pembahasan
Contoh Soal Fungsi Invers Komposisi Fungsi
Jika  dan
dan  maka
maka  adalah ….
adalah ….
Pembahasan:
Dengan cara cepat mencari fungsi invers, kita dapat secara mudah menentukan  .
.
Jawaban: A
Sumber : https://idschool.net






0 comments:
Post a Comment